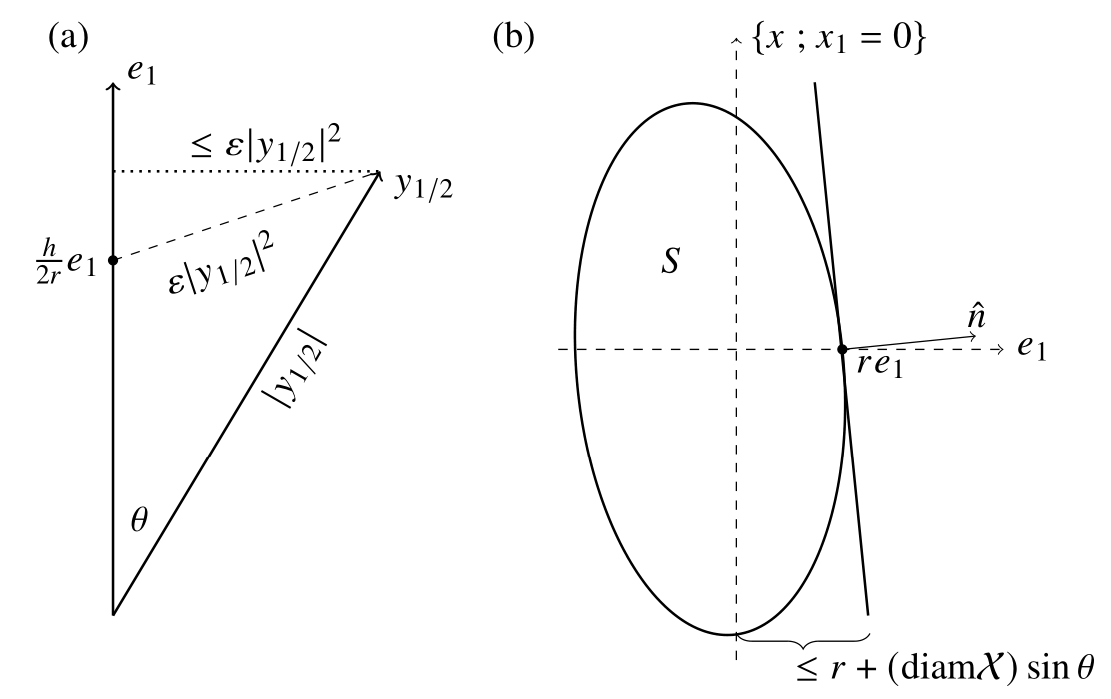
We prove the interior $C^{\mathrm{1,1}}$ regularity of solutions to a subclass of principal-agent problems originally considered by Figalli, Kim, and McCann. Our approach is based on construction of a suitable comparison function which, essentially, allows one to pinch the solution between parabolas. The original ideas for this proof arise from an earlier, unpublished, result of Caffarelli and Lions which we adapt here to general quasilinear benefit functions. For $C^1$ regularity of general quasilinear benefit functions, see Chen (2013, 2023). And for $C^1$ regularity of bilinear benefit function, see Carlier and Lachand-Robert (2001).

To appear soon.

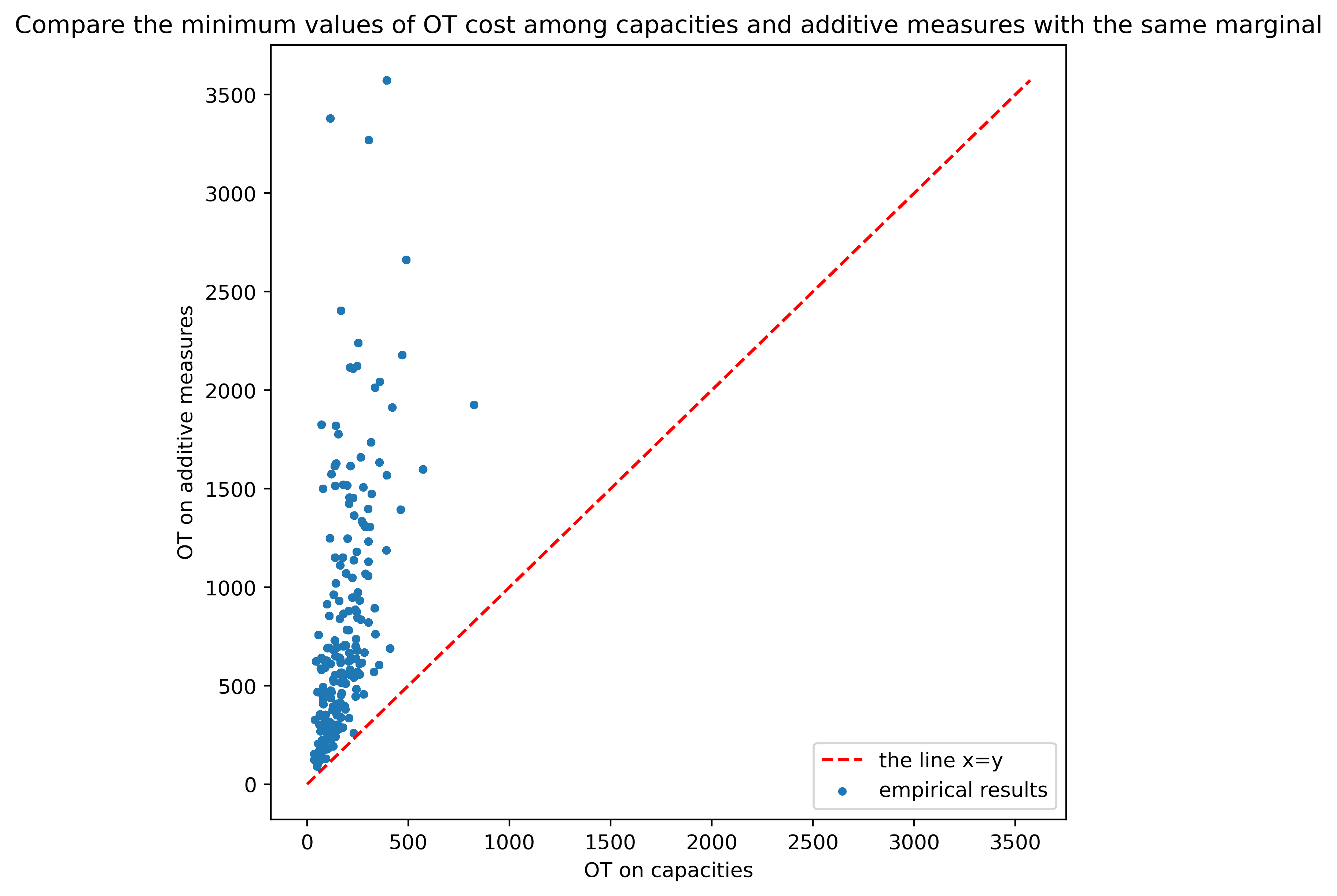
We investigate the problem of finding upper and lower bounds for a Choquet risk measure of a nonlinear function of two risk factors, when the marginal distributions of the risk factors are ambiguous and represented by nonadditive measures on the marginal spaces, but the joint nonadditive distribution on the product space is unknown. We treat this problem as a generalization of the optimal transportation problem to the setting of nonadditive measures. We provide explicit characterizations of the optimal solutions for finite marginal spaces, and we investigate some of their properties. We further discuss the connections with linear programming, showing that the optimal transport problems for capacities are linear programs, and we also characterize their duals explicitly.

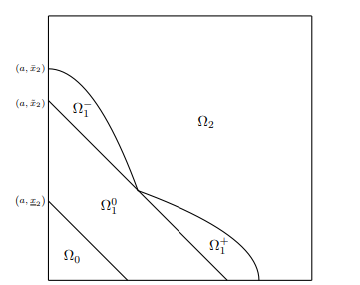
Adverse selection is a version of the principal-agent problem that includes monopolist nonlinear pricing, where a monopolist with known costs seeks a profit-maximizing price menu facing a population of potential consumers whose preferences are known only in the aggregate. For multidimensional spaces of agents and products, Rochet-Chone (1998) reformulated this problem to a concave maximization over the set of convex functions, by assuming agent preferences combine bilinearity in the product and agent parameters with a quasilinear sensitivity to prices. We characterize solutions to this problem by identifying a dual minimization problem. This duality allows us to reduce the solution of the square example of Rochet-Choné to a novel free boundary problem, giving the first analytical description of an overlooked market segment.

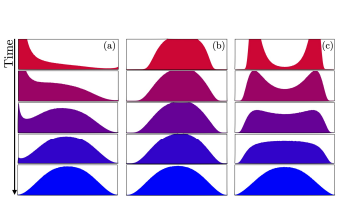
Discretized Langevin diffusions are efficient Monte Carlo methods for sampling from high dimensional target densities that are log-Lipschitz-smooth and (strongly) log-concave. In particular, the Euclidean Langevin Monte Carlo sampling algorithm has received much attention lately, leading to a detailed understanding of its non-asymptotic convergence properties and of the role that smoothness and log-concavity play in the convergence rate. Distributions that do not possess these regularity properties can be addressed by considering a Riemannian Langevin diffusion with a metric capturing the local geometry of the log-density. However, the Monte Carlo algorithms derived from discretizations of such Riemannian Langevin diffusions are notoriously difficult to analyze.

This paper considers Langevin diffusions on a Hessian-type manifold and studys a discretization that is closely related to the mirror-descent scheme. We establish for the first time a non-asymptotic upper-bound on the sampling error of the resulting Hessian Riemannian Langevin Monte Carlo algorithm. This bound is measured according to a Wasserstein distance induced by a Riemannian metric ground cost capturing the squared Hessian structure and closely related to a self-concordance-like condition. The upper-bound implies, for instance, that the iterates contract toward a Wasserstein ball around the target density whose radius is made explicit. Our theory recovers existing Euclidean results and can cope with a wide variety of Hessian metrics related to highly non-flat geometries.

We prove an existence result for the principal-agent problem with adverse selection under general assumptions on preferences and allocation spaces. Instead of assuming that the allocation space is finite dimensional or compact, we consider a more general coercivity condition which takes into account the principal’s cost and the agents’ preferences. Our existence proof is simple and flexible enough to adapt to partial participation models as well as to the case of type-dependent budget constraints.

This paper generalizes the approach of Carlier (2001) and provide an existence proof for the multidimensional screening problem with general nonlinear preferences. We first formulate the principal’s problem as a maximization problem with G-convexity constraints and then use $G$-convex analysis to prove existence.

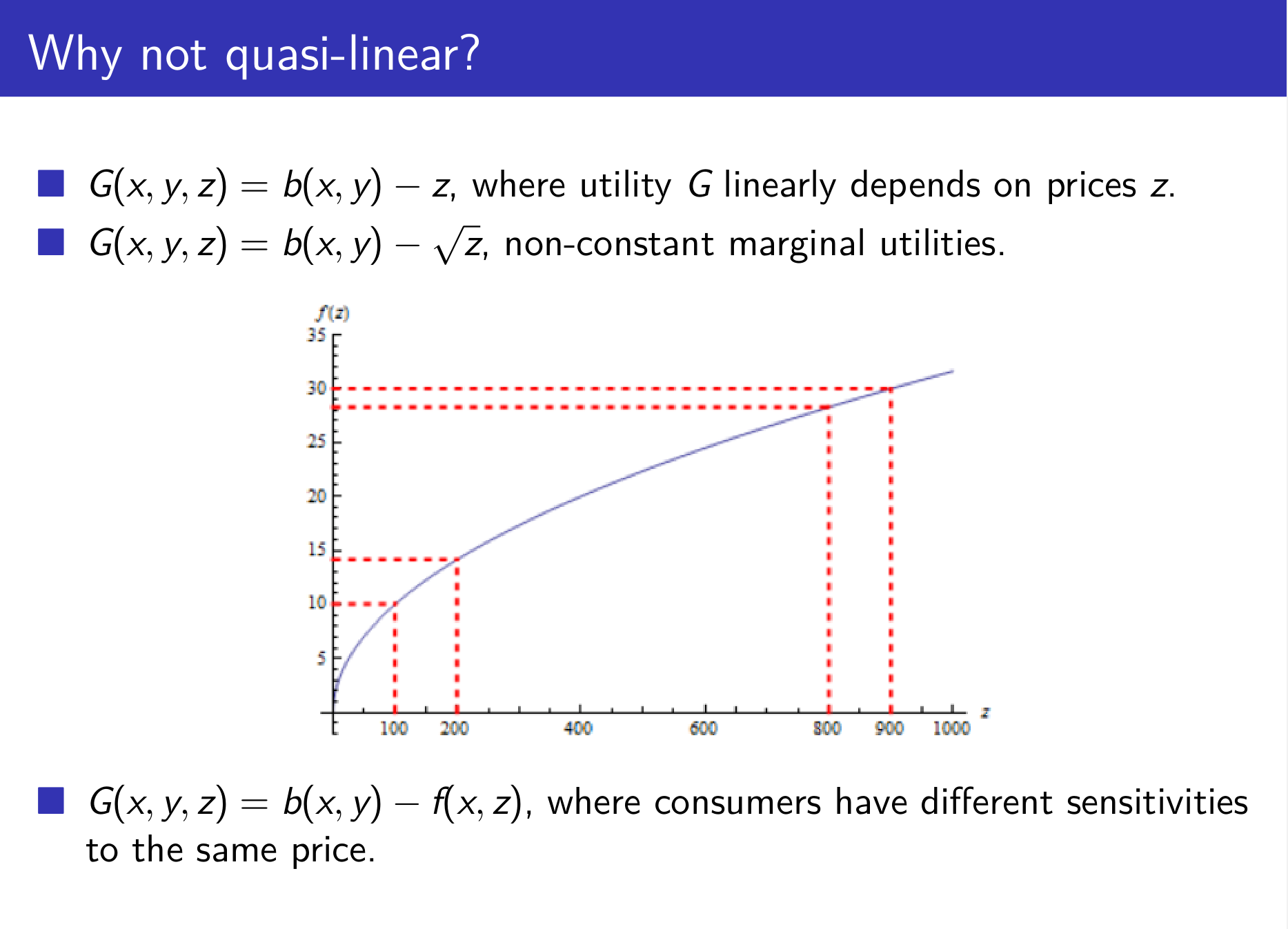
A monopolist wishes to maximize her profits by finding an optimal price policy. After she announces a menu of products and prices, each agent $x$ will choose to buy that product $y\mathrm{(}x\mathrm{)}$ which maximizes his own utility, if positive. The principal’s profits are the sum of the net earnings produced by each product sold. These are determined by the costs of production and the distribution of products sold, which in turn are based on the distribution of anonymous agents and the choices they make in response to the principal’s price menu. In this paper, we provide a necessary and sufficient condition for the convexity or concavity of the principal’s (bilevel) optimization problem, assuming each agent’s disutility is a strictly increasing but not necessarily affine (i.e., quasilinear) function of the price paid. Concavity, when present, makes the problem more amenable to computational and theoretical analysis; it is key to obtaining uniqueness and stability results for the principal’s strategy in particular. Even in the quasilinear case, our analysis goes beyond previous work by addressing convexity as well as concavity, by establishing conditions which are not only sufficient but necessary, and by requiring fewer hypotheses on the agents’ preferences. For the concavity results of quasilinear utility functions, see Figalli-Kim-McCann (2011).

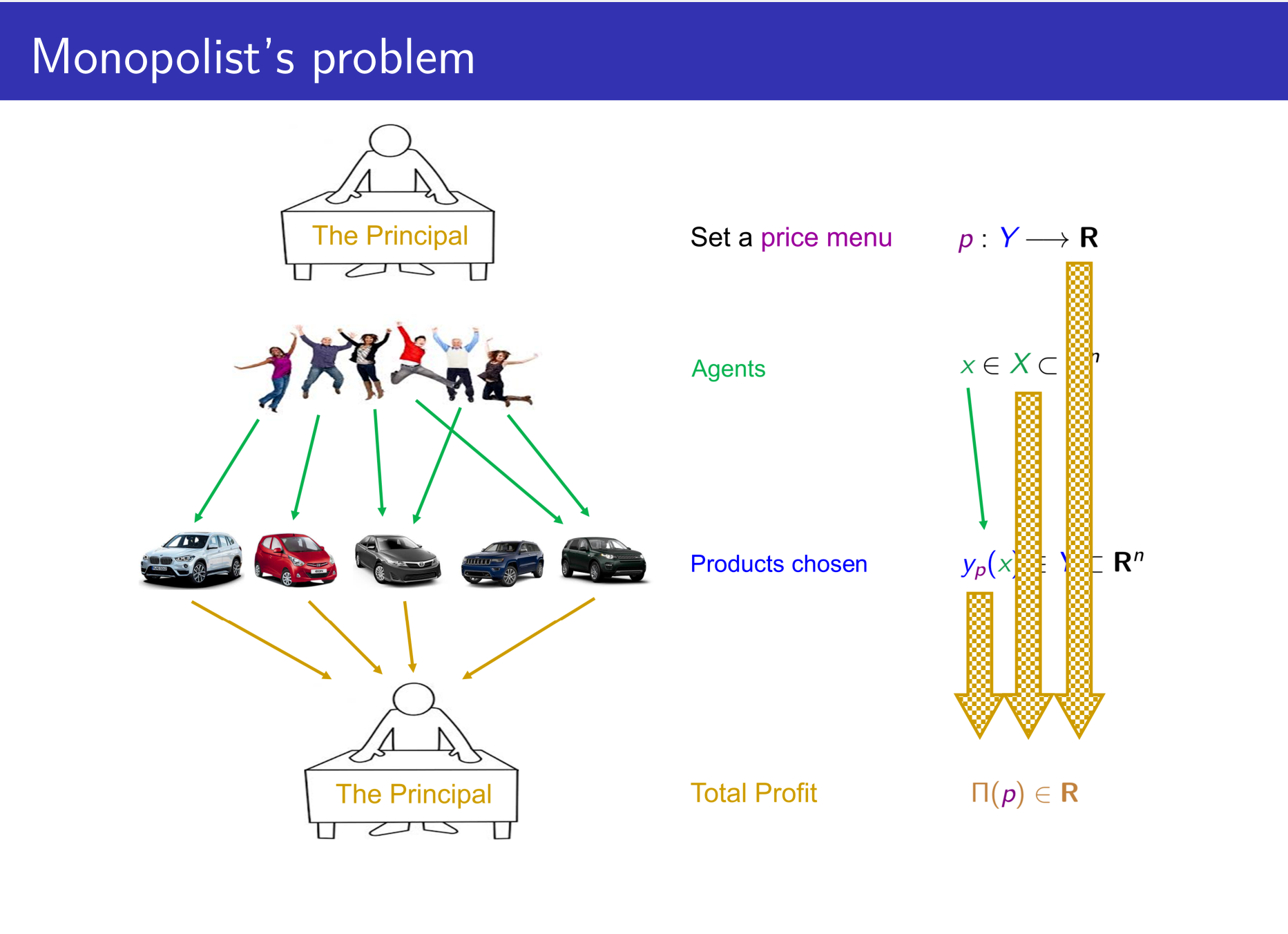
A monopolist wishes to maximize her profits by finding an optimal price menu. After she announces a menu of products and prices, each agent will choose to buy that product which maximizes his utility, if positive. The principal’s profits are the sum of the net earnings produced by each product sold. These are determined by the costs of production and the distribution of products sold, which in turn are based on the distribution of anonymous agents and the choices they make in response to the principal’s price menu. In this thesis, two existence results is provided, assuming each agent’s disutility is a strictly increasing but not necessarily affine (i.e., quasilinear) function of the price paid. This has been an open problem for several decades before the first multi-dimensional result obtained here and independently by Nöldeke-Samuelson (2018).

Additionally, a necessary and sufficient condition for the convexity or concavity of this principal’s (bi-level) optimization problem is investigated. Concavity when present, makes the problem more amenable to computational and theoretical analysis; it is key to obtaining uniqueness and stability results for the principal’s strategy in particular. Even in the quasilinear case, our analysis goes beyond previous work by addressing convexity as well as concavity, by establishing conditions which are not only sufficient but necessary, and by requiring fewer hypotheses on the agents’ preferences. Moreover, the analytic and geometric interpretations of a specific condition relevant to the concavity of the problem have been explored.

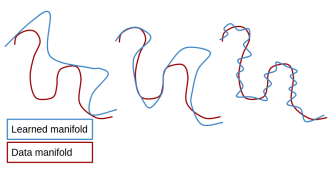
This paper raises an implicit manifold learning perspective in Generative Adversarial Networks (GANs), by studying how the support of the learned distribution perfectly match with the support of the real data distribution. We show that optimizing Jensen-Shannon divergence forces perfectly match of them, while optimizing Wasserstein distance does not. On the other hand, by comparing the gradients of the Jensen-Shannon divergence and the Wasserstein distances ($W_1$ and $W_2^2$) in their primal forms, we conjecture that Wasserstein $W_2^2$ may enjoy desirable properties such as reduced mode collapse. It is therefore interesting to design new distances that inherit the best from both. For pioneer papers on Wasserstein Generative Adversarial Network, see Arjovsky-Chintala-Bottou (2017) and Gulrajani et al. (2017).

Nowadays in modern medicine, computer modeling has already become one of key methods toward the discovery of new pharmaceuticals. And virtual screening is a necessary process for this discovery. In the procedure of virtual screening, shape matching is the first step to select ligands for binding protein. In the era of HTS (high throughput screening), a fast algorithm with good result is in demand. Many methods have been discovered to fulfill the requirement. Our method, called “Circular Cone”, by finding principal axis, gives another way toward this problem. We use modified PCA (principal component analysis) to get the principal axis, around which the rotation is like whirling a cone. By using this method, the speed of giving score to a pocket and a ligand is very fast, while the accuracy is ordinary. So, the good speed and the general accuracy of our method present a good choice for HTS.